Table of Contents
Table of ContentsCryptography Talk
These are notes for my guest lecture on cryptography presented to POL 599: U.S. Intelligence & Foreign Policy, on November 28, 2006 at the University of Miami. I thank Visiting Professor James Kilpatrick and his students for giving me the opportunity to make the presentation.
In this talk we will cover the following topics:
- Classical Cryptography
- Public Key Cryptograpy
- Further Advances in Cryptography
- Quantum Cryptography
We will give the student a technical overview of these topics. We will look at the emergence of cryptography into a modern, mathematical discipline, core to the subject matter of information sciences, with overlap in many other areas of science. We will overview some of the political struggles cryptography has encountered during this transformation.
Classical Cryptography
Classical cryptography was most concerned with confidentiality, the keeping of secrets secret. In this form, cryptography is very old. The Wikipedia History of Cryptography page defines classical cryptography a bit narrower than this, but it is a good additional reference to this material.
The first published work is Steganographia, by an alchemist named Trithemius. Although written earlier, the book was published in 1606. At this point in time, cryptography was closely allied to magic. However, cryptography has long retained that connection. During WWII, intelligence derived from the broken Japanese PURPLE cipher was code named Magic .
Methods for confidentiality are classed as codes, ciphers , or
steganography. A cipher is a general method for obscuring text, easily
reversable with the use of a key. The simplest ciphers are hand
ciphers. The mechanisms of hand ciphers can be done by a person using
pencil and paper. Various hand ciphers were in use during WWII, such as
the Playfair, despite their insecurity.
Some example classical hand ciphers
are provided by the Kryptos sculture.
Several cryptographers succeeded in a ciphertext only attack on very
limited sample material without prior knowledge of the mechanism. There
are four sections to the sculpture. Sections one and two use a sort of
Vignere, and the third uses a transposition cipher. The fourth section
remains a mystery.

An early modern work in cryptography is the still influential Cryptographie Militaire by Auguste Kerckoffs (1883). Kerckhoffs was a linguist, and so by this time was can consider that cryptography had passed from the hands of the alchemists to the linguists. Many early cryptographic endeavors, such as the breaking of the Rosetta stone, were accomplished by linguists, and in general, the literary crowd. However, in this paper Kerchkhoffs refers to ciphers which should be “substantially, if not mathematically, undecipherable.” Mathematics had begun to intrude on the discipline.
Just prior to WWII, developments in radio transmission and general human cleverness in building complex machinery made enciphering machines important and common. At about the same time, mathematicians were reevaluting the foundations of the field, and it was becoming clear that thought itself might be mechanizable. These events came together with invention of and the cryptologic breaking of the machine called the Enigma.
The Enigma resembled a typewriter with keys to be pressed, but had a family of lamps, labeled with the same letters as the keys. However, pressing a key, say A, made a different letter light, say M, depending on the position of a set or rotors. These rotors mapped the letters so that the typed message became scrampled, encrypted. The same machine can be used to decrypt the message. An Enigma encrypted message, when typed into the Enigma device a second time, with the rotors set the same as for encryption, would undo the encryption, and the original typed message would reappear.
The discovery of the pattern of mapping was confounded by the fact that there were several different rotors to use, and the rotors could be placed into the machine in different orders. Also, the rotors can be started in different positions. This meant that there was a wide range of mappings to start with, and the mappings changed with every keystroke. The German army and the German High Command depended on the Enigma to keep its communications secret.
The task of breaking the secrets of the Enigma required the participation of many people. The early work was done in Warsaw by a Polish mathematician Marian Rejewski. The Polish were conscious that German would soon attack and carefully tracked cryptological developments in order to get hints as to what sort of ciphers would be used. Rejewski had a general notion of how the Enigma was constructed, but had to build a replica himself without knowing any of the details of the construction.
After Poland was invaded, Rejewski and his group fled to France and later England. Copies of his recreation of the Enigma were given to the British and they continued work on the cryptanalysis at Bletchley Park. Here the very famous mathematician Alan Turing made important discoveries. Alan Turing is also considered to be the father of computer science, and the creator of the Turing Machine, an abstract model of modern computers, and in fact, of all abstract reasoning.
In addition to mathematical analysis, primitive computers were also used to help break the Enigma. Rejewski had created a Bombe, and this was extended at Bletchley and later in the USA. This work was kept secret until 1970. Now work has begun on reconstructing the computers created during this time period, including a reconstruction of Turing's Bombe.
As sophisticated as the Enigma was, it was still a classical cipher working on similar principals as simple hand ciphers, as epitomized by the CIA’s Kryptos sculture, or the powerful commercial ciphers currently in used, such as DES, the Data Encryption Standard, created in 1976
The Data Encryption Standard, or DES. This is an encryption algorithm made at IBM by a team lead by Horst Feistel. In 1976 the algorithm was accepted by the National Institute of Standards and Technology as the standard algorithm for securing commerical data, such as financial transactions between banks. Although the algorithm was created by a distinguished list of civilian cryptographers and mathematicians, the development was helped or interfered with by the National Security Agency.
Mathematical Theory of Cryptography
There are three main types of encryption:
- Codes
- Steganography
- Ciphers
Codes are a set of replacements for words, and are dependent on a codebook. They are effective, however, they can be broken just as any encryption. Steganography is the a secrecy of a message by hiding it in plain view. Ciphers are general mechanisms for the transformation of text whose secrecy depends on a small key. In most applications, ciphers are perfered over codes and stego for practical reasons: unlike codes there are not fixed codebooks, and it is fast and easy to distribute new keys if a key is compromised. Unlike stego, the messages are easily sent by radio or any simple communication channel.
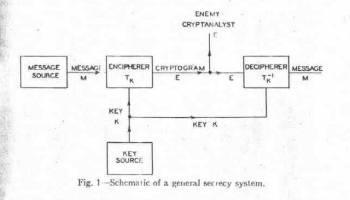
A cipher consists of a pair of mechanisms, be they simple or complex, mechanical or computerized, manual or automatic, which transforms the message as written, called the plaintext into its encrypted form, called the ciphertext, and back again. This process is guided by the two party’s understanding of the mechanism used and an additional piece of information, called the key. The enemy observes the ciphertext, and might even have full knowledge of the mechanism of encipherment and decipherment, but does not know the key. This description is shown in Communication Theory of Secrecy Systems by Claude Shannon, published in 1949. Some consider this the founding document of modern civilian cryptography. Here is a page of the document and an enlargement of the diagram showing a cipher system.
To break a cipher means to find a practical method to extract the meaning from an encrypted message. In most cipher systems there is a large but ultimately finite number of different keys. In most situations it is intellectually possible to try all keys, until one is found for which the encrypted message reappears as a sensible text. More wildly optimistic, perhaps on one or several tries of random keys, the correct keys is magically guessed. These exhaustive or lucky methods are not considered to have broken a cipher.
To break a cipher means to do better. To have a method with a significantly greater possibility of success in a very much shorter time frame than the above luck and brute force methods. The break could be a method to recover only the message. It might be a method to recover the key! Such a method is called a complete break. Attempts to break a cipher are categorized as:
- Ciphertext only: we are only given encrypted material to work with.
- Known plaintext: we are given both encrypted material and the text that material encodes. There might be several methods to manage these situations. One might even guess at possible plaintext, or rely on common patterns of speech or letter writing.
- Chosen plaintext: the breaker is allowed in active role to suggest plaintext to be encrypted and then have access to the resulting encryption. This situation might be managed by planting information by espionage and watching for the result on monitored lines.
Very weak cipher systems yeilds complete breaks using a ciphertext only attack. Stronger systems might require massive amounts of chosen plaintext to analyze and extract the key.
The Crypto Wars
Since the founding of the NSA (also known as the “No Such Agency” agency) in 1952 by President Truman, there has been a question as to the legal status of civilian cryptography. As electronic communication and especially banking became prevalent, there was a need for secure communications. To some extent, the government was reluctant to cede control over the use of and knowledge about encryption. DES was created by IBM to be a standard commercial encryption for banking. It was developed in collaboration with the NSA and for years there were questions about NSA’s role in the collaboration.
As the date at which DES was made a national standard for encryption and the date of announcement of the creation of Public Key Cryptography by Whitfield Diffie and Martin Hellman, 1976 marks the beginning of some difficult decisions by the government concerning the direction and accessibility of cryptography for and by civilians. This period is called the Cryptography Wars. The reference to read concering this is Privacy on the Line by Whitfield Diffie and Susan Landau. Also University of Miami Law Professor Michael Froomkin was very much involved in this topic (see It came from planet clipper: The battle over cryptographic key escrow).
In a short period of time, cryptography went from an occult art or literary pastime to a mathematical science integrally linked to the information age and of great political interest to the government. The government exercised two forms of restraint on civilian cryptography. First, prior restraint: research on cryptography may have had to be reviewed by the government, and the the government must permit publication. Second, cryptographic equipment is considered either a munition, and its export is controlled by the Department of State subject to the Arms Export Control Act and the International Traffic in Arms Regulation (ITAR), or a dual-use item, and its export is controlled by the Department of Commerce subject to the Export Administration Act.
This became an issue as the effective life of the DES standard drew to a close. DES, created in a respectful and enlightened collaboration between IBM and the NSA, was an effective cipher. It is limited, however, by its short key length. All ciphers have keys, and guessing the key, or finding the key by trial and error, is always a threat, lessened by the fact that there are some many keys to try. For DES, there are 72,057,594,037,927,936 keys (this is called 56-bit security). In 1976 this was a lot of keys. Computers in those years would take centuries to search through the key space. In 1998 a group called the Electronic Freedom Foundation built a $250,000 computer that took 56 hours to complete the search. A new standard encryption algorithm was needed.
The United States government was wary of a new algorithm that was too strong. At the time, encryption in excess of 80 bit keys could not be exported. On the other hand, commerce demanded good security. Companies such as Sun opened up development offices outside the United States for their cryptographic development. Meanwhile, in 1993 the United States government suggested the use of Key Escrow and the NSA secret Skipjack algorithm in the tamper-proof Clipper Chip as a compromise.
To add to the excitment, in 1994 the NSA algorithm was cracked by Matt Blaze, an AT&T researcher. Eventually encryption policy was liberalized and an open, participatory process for the successor to the DES standard was initiated under the jurisdiction of the National Institute of Standards and Technology. This resulted in the Advanced Encryption Standard, the current government certified cipher for commerical use.
Public Key Cryptography
With the pressing development of electronic communication and commerce during the 1970’s there came a need for cryptography to replicated in the digital domain certain customary rituals in the physical domain. The first, to assure private communications between two parties which up to the moment of conversing had no prior contact. The second, to provide an electronic equivalent of a signature. That is, a numerical tag to a message which proves the identity of the of the sender of a message, as well as obliges the signer to the content of the message.
The first ritual is a form of confidentiality, and is a traditional aim of cryptography. However, the problem posed is not solvable by classical codes and ciphers, all of which require that the communicating parties meet ahead of time, in person, and in secret, to exchange completely private keys.
The second ritual involves completely new concerns for cryptography: authenticity, methods for determining that a document is from a certain party; integrity, methods to determine that a document has not been altered; and non-repudiation, methods that permit any third party to agree that the document is from a certain party and not been altered. Classical codes and ciphers can be helpful to establish authenticity and integrity - it should be as difficult to break an encyption as to produce a falsely encrypted message (presumable, but maybe not). However, with a shared private key it is impossible that a third party can resolve any dispute, let alone assure that the third party is not acting in collusion with one of the disputant parties.
These problems were solved with the invention of public key cryptography, announced by Whitfield Diffie and Martin Hellman in New directions in cryptography (PDF), published in 1976. (A more complete description of the development of public key is given in The first ten years of public-key cryptography by Whitfield Diffie (1988)(PDF).)
In the 1976 paper, Diffie and Hellman:
- defined conceptually the propeties a public key crytosystem;
- they defined a type of mathematical function called one-way trapdoor functions, and showed how a public key cryptosystem can be based on such functions; and
- they presented a specific protocol, now known as Diffie-Hellman, to accomplish the exchange of a private key over a public channel.
The Diffie-Hellman key exchange protocol presented in this paper is currently used in every secure and e-commerce web site in the world, and is the basis for successful e-commerce. It is used when you log into myum, when you bank on the internet, or make any internet purchase.
The Diffie-Hellman protocol uses one-way functions, not one-way trapdoor functions. Diffie-Hellman did not know how to construction such functions. However, the next year Ron Rivest, Adi Shamir and Len Adleman found a one-way trapdoor function and with that created the RSA public key cryptosystem. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems by Ron Rivest, Adi Shamir and Len Adleman (PDF). This system is the most popular public key crypto system in use and does encryption and signatures.
The idea of public key
 Classical ciphers have a single, shared, private key. They are called
symmetric key ciphers because the single key is used both to encrypt
and decrypt. The idea of public key is to have two keys, one for
encryption the other for decryption. The encryption key is made public,
hence the name, public key cryptography. The decryption key is kept
secret. As far as is known, if the encryption-decryption function is
one-way trapdoor, there is no known way to figure out what the secret
key is given the public key.
Classical ciphers have a single, shared, private key. They are called
symmetric key ciphers because the single key is used both to encrypt
and decrypt. The idea of public key is to have two keys, one for
encryption the other for decryption. The encryption key is made public,
hence the name, public key cryptography. The decryption key is kept
secret. As far as is known, if the encryption-decryption function is
one-way trapdoor, there is no known way to figure out what the secret
key is given the public key.
 Suppose Bob wants to send a private message to Alice, but has never yet
communicated with Alice. Alice has created both an encryption and a
decryption key and has made the encryption key public and available to
everyone on the internet. Bob encrypts his message with this key and
sends the encrypted message to Alice. Alice uses her decryption key to
recover the message. No one else can decrypt the message. Only Alice
has the decryption key and that is kept secret.
Suppose Bob wants to send a private message to Alice, but has never yet
communicated with Alice. Alice has created both an encryption and a
decryption key and has made the encryption key public and available to
everyone on the internet. Bob encrypts his message with this key and
sends the encrypted message to Alice. Alice uses her decryption key to
recover the message. No one else can decrypt the message. Only Alice
has the decryption key and that is kept secret.
As  was observered by Diffie and Hellman, the same public key system can be used to create a Digital Signature.
In this case the private key is the signing key and the public key is
the verification key. To sign a message, Alice uses the private key. If
Bob, or any party, wishes to verify that the message is truely from
Alice, they use the public key to recover the signed message. Only
Alice could have created the signed version of the message, only she
has the private key to do that. However, anyone can use the public key
to verify the message and to hold Alice accountable for the contents.
was observered by Diffie and Hellman, the same public key system can be used to create a Digital Signature.
In this case the private key is the signing key and the public key is
the verification key. To sign a message, Alice uses the private key. If
Bob, or any party, wishes to verify that the message is truely from
Alice, they use the public key to recover the signed message. Only
Alice could have created the signed version of the message, only she
has the private key to do that. However, anyone can use the public key
to verify the message and to hold Alice accountable for the contents.
Diffie-Hellman Key Exchage
The  Diffie-Hellman protocol in their paper does not actually use the
trapdoor property, only one-wayness. The public key for each Alice and
Bob is created from the secret key using a function which cannot be
easily undone. Alice creates a new random key, passes through the
one-way function and publicly gives Bob the result. Bob does likewise.
Now each Bob and Alice is in possession of their own secret key and the
other’s public key. Any bystander has knowledge of both public keys but
of neither secret key, because the function is one-way. The type of
one-way function proposed by Diffie-Hellman allows each Alice and Bob
to combine what they know to generate a common secret. This secret is
not known to any one else, since it requires knowledge of at least one
of the private keys. This common secret is used as a key in any
standard symmetric cipher for the ongoing, private, communication
between Alice and Bob.
Diffie-Hellman protocol in their paper does not actually use the
trapdoor property, only one-wayness. The public key for each Alice and
Bob is created from the secret key using a function which cannot be
easily undone. Alice creates a new random key, passes through the
one-way function and publicly gives Bob the result. Bob does likewise.
Now each Bob and Alice is in possession of their own secret key and the
other’s public key. Any bystander has knowledge of both public keys but
of neither secret key, because the function is one-way. The type of
one-way function proposed by Diffie-Hellman allows each Alice and Bob
to combine what they know to generate a common secret. This secret is
not known to any one else, since it requires knowledge of at least one
of the private keys. This common secret is used as a key in any
standard symmetric cipher for the ongoing, private, communication
between Alice and Bob.
The mathematics of public key
The creating of public key cryptography requred two things: the conceptual idea and actually mathematical functions which are one-way, and one-way trapdoor. The mathematics is in finding such functions and showing that they are in fact one-way or one-way and trapdoor. So far, appropriate functions are the found in the subject of Number Theory. Number Theory is essentially the mathematics of whole numbers, 1, 2, 3, and so forth. And particularly about the properties of certain of these numbers, called prime numbers.
A prime number cannot be expressed as the product of other numbers. For instance, 7 is prime but 6 is not. A sort of one-way function is multiplication: given two primes, p and q, it is easy enough to multiply them together and get the product n = pq. On the other hand, given a number n, even knowing that there are primes p and q which multiply to n, there is no known fast way to find these primes. From wikipedia: NSA’s budget for electricity exceeds US$21 million per year [citation needed], making it the second largest electricity consumer in the entire state of Maryland. That’s because at the NSA they are trying to find primes p and q such that they multiply to (the Kremlin’s) n.
So Alice can generate large primes p and q and that will be her secret. She will multiply them together and make public the product n. How does she use these keys to encrypt? Alice needs two more numbers, one called the encryption exponent e, which she will make public, and the other called the decryption exponent d, which she will keep secret. She choses one of them, say d, at random, with value between 1 and n-1, and then computes the other, in this case e, so that ed-1 is a multiple of (p-1)(q-1).
To encrypt a message to Alice, Bob takes his message m, conveniently rendered into a number between 0 and n-1, and takes it to the power e, that is, he multiplies m with itself e times, and then reduces the result to the remainder when divided by n. As described, this would be time consuming, but there are very fast ways of doing this. He sends the result to Alice.
To decrypt this message, Alice takes the encrypted message and multiplies it with itself d times, reducing the result to the remainder when divided by n. By a theorem in number theory, called Little Fermat, this will decrypt the message.
This is the RSA crypto system. Here is an example. (From the original RSA paper). Let p be the prime 47, and q be the prime 59, and d, the decryption exponent be 157. Alice will keep all of this information secret. The product of the primes is n=2773, and it turns out that the encryption exponent e corresponding to all the secret information is e=17. (Note that de-1=2668=(p-1)(q-1), as required for d and e.) Alice makes this n and e public.
Suppose Bob wants to tell Alice the message 13. 13 multiplied to itself 17 times is something big: 8650415919381337933. When divided by 2773, its remainder is 219. The encrypted message sent by Bob to Alice is 219. Alice decrypts by raising 219 to the 157 power and dividing by 2773, only keeping the remainder. In order to do this there are several tricks: tricks to raise to a power quickly, and tricks to constantly divide away 2773 so that no intermediate result ever gets too big. Once this is done the result is 13. Alice has Bob’s message.
The security of RSA is that it is hard to factor a large number. On the surface, it seems that the secrecy is in the number d, in this case 157, and not in the values p and q. It turns out that if p and q are known, then d is easily calculated from them and e, and if d and e are known then it is easy to find the factors p and q of n. So figuring out d from n and e is of the same difficulty as figuring out p and q from n and e.
In this example, 2773 is a small number, and we could use a computer to factor it, thereby finding Alice’s secret. In actual use, however, p and q are very large numbers, hundreds of digits long. The longer the better. Web sites which use RSA will provide certificates of 1024 bits (that is a number with about 300 digits).
Certificates
The Diffie-Hellman algorithm is used in the secure web browsing protocol, called https, to create a new secret key between a browser and a server at the start of a browsing session. Once the key has been created, it is then used to encrypt the communication using a symmetric cipher. DES is now considered too weak so other ciphers are used. The official candidate is AES, but other popular ciphers are triple DES (DES done three times, to make it stronger) and RC4 (a symmetric stream cipher). The choice is made by the browser and server configuration.
There has been an effort to educate users about the need to use secure http, for example, when doing on line banking. Various icons and color changes appear when a page is secure.
The use of a digital signature is understood in the context of on-line banking. Using Diffie-Hellman we know that we are talking securely to the software at the other end of the wire, but we have no idea who is at the other end of the wire. The https protocol also provides a method using public key cryptography for authenticating the server. It does this using certificates.
Web sites wishing to prove their identity to a browser register with a Certificate Authority, or CA. The CA will generate a public/private key pair and create a certificate naming the web site, the company name, and the public key, all signed with the CA’s own private key. Some big CA’s are Verisign, Thawte and Entrust
Suppose a browser wishes to authenticate the server. This is certainly done for an on-line banking application, that is, I now want the server to prove to me that it’s Citibank, not some hacker site. After key exchange, which only establishes confidentiality, the browser produces a random document and challenges the server to sign it properly. The valid server does so, returning both the signed document and its certificate.
The certificate is provided in case the browser does not know the public key of the site already. First the browser verifies the certificate using the public key of the CA. CA’s are well known, and their public keys are shipped built into any browser (Firefox → Preferences → Advanced → Security → View Certificates → Authorities, other browsers have similar) (and what if someone tampers with you browser?). Knowing now that the public key is valid, it checks the signature on the document. If all goes well, we proceed, confident that the server is who it says it is. Or at least that it is in possession of a secret which the CA has said only the server knows.
This does depend both on the integrity of the browser software and of the CA’s proceedures to issue certificates.
Prior Art
Although 1976 was the public invention of public key, it appears that at least the British government cryptologists had discovered it earlier. Government Communications Headquarters (GCHQ) is the British equivalent of the American NSA. In the 60’s James Ellis had an idea for what he called non-secret encryption. In 1973 Clifford Cocks from GCHQ filled in the details to create the equivalent of RSA, and in 1974 M. J. Williamson created a scheme similar to Diffie Hellman.
Bruce Schneier has summarized the situation in a Dr. Doob’s article. James Ellis has also written his own History on non-secret encryption documenting the situation. It is claimed that the NSA knew of public key independently of the British but there have been no documents produced to substantiate the claim.
Further Advances in Cryptography
Since the introduction of public key, computer science and cryptography as co-evolved to encompass many more areas than confidentiality, authenticity, integrity and non-repudiation. Computation is a natural phenomena, like gravity or light, and follows natural laws. Cryptography is a natural partner to computer science in exploring the nature of information and communication.
For instance, cryptographers now has methods for two players to flip a coin by conversing over the telephone: neither player has to trust the other, both agree on the outcome, which was a fair outcome, and both sides know it was fair.
Zero Knowledge
Or the method of zero knowledge, introduced in 1985, in which two players, a Prover and a Verifier, have a discussion during which the Prover convinces the Verifier of a fact, but at the same time, the Verifier learns nothing about the fact, other than that it is a true fact.
As an illustration of how zero knowledge might work, and where it could be useful, consider the problem of identification. I, as the Prover, will prove to you, as the Verifier, my identity. However, I don’t want to divulge anything about myself to you, perhaps I am concerned that you will use any such information to later impersonate me to a third party.
For instance, I could produce an ID card which you check, but then you learn a lot of information about me, you might even copy the ID card and use it yourself! So this is not zero-knowledge. In a zero-knowledge protocol identity would be established through a conversation in which I reveal nothing about myself to you, yet at the end of the conversation you are rightly convinced of my identity.
Such a protocol would consist of me reminding you about things which you already know about me. These are things only we two know, and somehow (in the protocol this works out) I never error by “reminding” you about something which you didn’t know, hadn’t noticed, or didn’t remember. In such an interaction, you learn nothing. You could have revealed these souvenirs to a third party whether or not we had our walk down memory lane, you already knew these things. But also, they prove nothing to the third party, they are random, perhaps fanciful vignets of no value.
In the digital world it is in fact possible to set up a situation where any two strangers have a supply of such personal memories that can be used in this manner.
A dating game
Describing the theory of zero knowledge is very complex. Instead I would like to describe a similar protocol, and one that solves a similar knowledge release problem using a simple deck of cards. This also shows that cryptography is not only about complicated computations on powerful computers, it is about the nature of information and communication.
Suppose Alice and Bob have a friend Yenta who decides that maybe Alice and Bob should date, and says so publicly. Actually, maybe Alice and Bob should date. If the interest is mutual then there is no reason for them not to admit this to each other and publicly and go on a date. If the disinterest is mutual then things are probably not too complicated either. But how to approach this if one is interested and the other not, in such a way that nobody gives away their position?
The cryptographic question is to provide a method by which Alice and Bob publicly interact, after which both learn that they are both interested and have mutually agreed to date, or if one or both does not want to date, all they learn is that they have not mutually agreed to date. Public observers do not learn, in the latter case, if it the disinterest was mutual or not, or which one of the two liked the other. They only learn that it was not the case that they mutually agreed to date.
The situation for, say Alice, is a bit more subtle. If she is interested in Bob, but the result of the method is that they will not date, then she knows it was because Bob was not interested, else it would have been a mutual interest. However, she is assured that Bob does not know of her interest. Since he does not want to go on the date it is not necessary for him to learn Alice’s position, and our method will not provide this information to him. Likewise, if she does not want to date Bob, the result of the method is that they will not date, and she will not know whether or not it was because she alone did not want to date, or that the disinterest was mutual.
From a deck of playing cards select three hearts and two clubs. The cards should be identical except for color, so please ignore the actual value of the cards. If Alice or Bob is interested in a date, she or he places the heart on top of the club, else the club goes on top of the heart. Collect Alice’s cards, place a heart card on top, then reverse Bob’s card and place the pair on top. Now cut the cards.
She loves me:
She loves me not:
And neither do I love her:
There must be secrecy until the cards are cut. Cuts can be made by all participants, to assure a fair share in guarenteeing anonymity. Once the cut is made, the cards are turned over and viewed.
Either three hearts appear next to each other (considering the two ends of the deck to be neighbors) or they do not. If they are next to each other, Alice and Bob have a date! else they do not.
I think this is a very heart-warming application of cryptography, but it is also very serious. It allows for electronic negotiation of contracts. For instance, allowing someone to bid on a contract with the assurance that only the winning bid will be revealed - lower price bidders walk away without revealing their price.
Quantum Cryptography
Quantum Cryptography uses the principles of quantum physics to create a channel which is impossible to eavesdrop. A key exchange protocol using the polarization of light was invented in 1984 by Gilles Brassard and Charles Bennett. By 1989 they had made a working prototype.
Light is made up of photons, which are like small marbles. They have no mass and they travel at the speed of light. They have a polarization, like an axis of rotation, that can point in any direction. Light is generally a mixture of photons of any and all polarizations. Polaroid filters, like polaroid glasses, have a polarization direction and will let photons pass only if they are polarized in the same direction as the filter. If the photon is polarized at right angles to the filter it will be blocked.
But polarization is a quantum phenomena, and quantum phenomena act very strangely. Quantum phenomena cannot be in partial states. If a photon has a polarization at an angle to the direction to the filter it must either pass or be blocked. If it passes it will jump into alignment with the filter, if it is blocked it will jump into an alignment at right angles to the filter. It will do this at random with a bias according to how closely the photon is directed relative to the filter. Once the photon has jumped to its new orientation it is impossible to know anymore about the photon’s original orientation. In quantum physics, observations determined the observed.
The device prposed by Bennett and Brassard proposed to encode each bit
by the polarization of a photon according to one of two systems, the +
or the x.  If the + system is used, a 1 bit is encoded by a photon of up
polarization, and a 0 bit by across polaration. If the x system is
used, a 1 bit is encoded by a photon of diagonal polarization up and to
the left, and a 0 but diagonal polarization up and to the right. For
each bit,
If the + system is used, a 1 bit is encoded by a photon of up
polarization, and a 0 bit by across polaration. If the x system is
used, a 1 bit is encoded by a photon of diagonal polarization up and to
the left, and a 0 but diagonal polarization up and to the right. For
each bit,  Alice choses at random which of the two systems to use. Bob does not
know for each bit whether Alice was using the + or x system, so he
choses one randomly
Alice choses at random which of the two systems to use. Bob does not
know for each bit whether Alice was using the + or x system, so he
choses one randomly  and makes a measurement.
and makes a measurement.
The device was built by Bennet and Smolin, a visiting researcher to IBM. The photos of the device are from The early days of experimental quantum cryptography by Smolin, IBM Journal of Research and Development, January 2004.
If Bob guess right, he observers correctly the polarization of the photon and decodes Alice’s bit perfectly. If Bob guesses wrong, the photon will hit the filter at a 45 degree angle, regardless of its encodeing a 0 or 1, and jump to one of the two orientations with a completely random 50-50 probablity. That is, Bob gets a completely random coin flip instead of Alice’s bit.
Having collected so many bits, Alice then stops and announces to Bob publicly the systems + or x for each of the bits. Bob can then throw away all the observations he made with wrong guesses and keeps all the good observations. He can then tell Alice which of the observations are good and now Alice and Bob have communicated about half of the bits Alice sent.
Why do we do this? Suppose Eve attempts to listen in, taps the channel. She must observe the photons using either the + or x system. Each time she guesses wrong she distroys the information on the photon and cannot reconstruct the information to forge a new photon for Bob. If Eve taps the line she must destroy half of the information she receives.
So ok, Alice and Bob reconcile their measurement systems. Now they look for evidence of eavesdropping. Of the bits that were supposedly correctly received, Bob, again by public channel, reveals half to Alice. Alice determines what percentage of the bits are in error. These error bits are evidence of eavesdropping. The quantity of errors gives an approximate bound on the number of bits Eve has possibly tampered with.
So now, of the original bits, Bob and Alice have a quarter of them which were (a) measured correctly using + or + by Bob and (b) which were not revealed in order to guage the amount of wiretapping that had occured.
Now there is some mathematical magic. There is a function called privacy amplification which can squeeze out from these remaining bits any information which Eve could have learned. If, for instance, by looking at the error rate, we know Eve could have learned up to half of these bits, we can squeeze down the bit string to a quarter its size in such a way that what was thrown out was what Eve knew about the string. We can do this even though we don’t know exactly what bits Eve has learned, only that overall her knoweledge doesn’t exceed one half of the bits.
The 1989 device sent the first message protected by quantum cryptography a distance of 30 centimeters. Now BBN has built a quantum cryptographic network spanning the Boston area and companies such as ID Quantique, MagiQ and Toshiba sell commercial quantum cryptographic machines.
Endnotes
Initial version presented November 28, 2006.
© Copyright 2006 Burton Rosenberg, all rights reserved.
 Table of Contents
Table of Contents