Search Control

Consider the Z-to-A example below (the reverse of the class example). Trace the sequence of transformations for the "expanding all ways from a chosen state" approach, to get from Z to A, for a
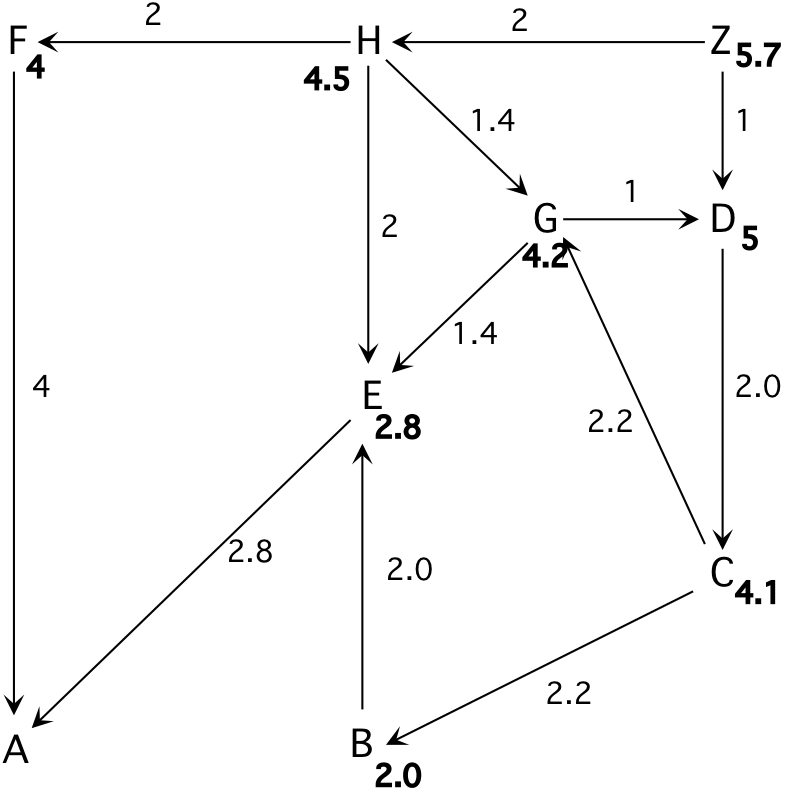
  1. Consecutively bounded depth first search to find any solution, depth increment 1. 
    Z
Z,D,H
Z,H,F,E,G,D,C
Z,H,F,A (done)
  2. Branch and bound search with dynamic programming. 
    Z(0)
Z-D(1),Z-H(2)
Z-H(2),Z-D-C(3)
Z-D-C(3),Z-H-G(3.4),Z-H-F(4),Z-H-E(4)
Z-H-G(3.4),Z-H-F(4),Z-H-E(4),Z-D-C-B(5.2),Z-D-C-G(5.2)
Z-H-F(4),Z-H-E(4),Z-H-G-D(4.4),Z-H-G-E(4.8),Z-D-C-B(5.2)
Z-H-E(4),Z-D-C-B(5.2),Z-H-F-A(8)
Z-D-C-B(5.2),Z-H-E-A(6.8),Z-H-F-A(8)
Z-H-E-A(6.8),Z-D-C-B-E(7.2),Z-H-F-A(8)
  3. Best first search, using the indicated estimated costs to the goal. 
    Z(5.7)
Z-H(4.5),Z-D(5)
Z-H-E(2.8),Z-H-F(4),Z-H-G(4.2),Z-D(5)
Z-H-E-A(0)
  4. The A* algorithm with dynamic programming. 
    Z(0+5.7)
Z-D(1+5),Z-H(2+4.5)
Z-H(2+4.5),Z-D-C(3+4.1)
Z-H-E(4+2.8),Z-D-C(3+4.1),Z-H-G(3.4+4.2),Z-H-F(4+4)
Z-H-E-A(6.8+0),Z-D-C(3+4.1),Z-H-G(3.4+4.2),Z-H-F(4+4)