The Search Problem
In the resolution procedure there are choices to be made
- Which chosen clause to use
- Which other clause to use
- Which literals to resolve upon
The combination of decisions made for these choices guide the search for a
refutation.
Given the decisions made, a single resolvant can be generated.
Regardless of the search strategy used, some mechanism is required to prevent
the same resolution step being repeated.
The basis of the ANL Loop (so named, as it was first used in ATP
systems developed at Argonne National Laboratory, the most famous of which
is now Otter), is to divide the resolvants that can be generated into plys.
Each ply contains resolvants that are the same number of resolution steps
away from input clauses.
Diagramatically, this can be thought of as follows :
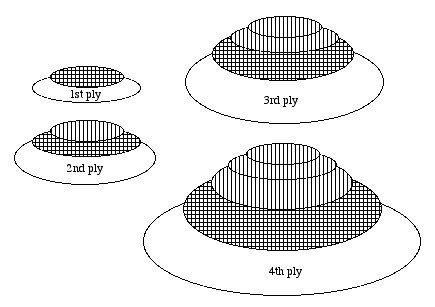
where at each iteration one parent is chosen from the cross-hatched area
and the other is chosen from the cross-hatched or vertical striped area.
The resolvants are put into the blank area, ready for the next iteration.
Evidently a duplication free search is being performed.
| Example
|
|---|
S1 = { p(b) | r(Y) | p(Y),
~p(S) | p(b),
~p(b),
~r(a),
~r(c) }
| 1st ply
|
| p(b) | r(Y) | p(Y)
|
+
|
~p(S) | p(b)
|
» |
r(Y) | p(Y) | p(b)
p(b) | r(Y) | p(b)
r(Y) | p(b)
|
|
|
+
|
~p(b)
|
» |
r(Y) | p(Y)
p(b) | r(b)
r(b)
|
|
|
+
|
~r(a)
|
» |
p(b) | p(a)
|
|
|
+
|
~r(c)
|
» |
p(b) | p(c)
|
| ~p(S) | p(b)
|
+
|
~p(b)
|
» |
~p(S)
|
| 2nd ply
|
| r(Y) | p(Y) | p(b)
|
+
|
~p(S) | p(b)
|
» |
r(Y) | p(b) | p(b)
r(Y) | p(Y) | p(b)
r(b) | p(b)
|
|
|
+
|
~p(b)
|
» |
r(b) | p(b)
r(Y) | p(Y)
r(b)
|
|
|
+
|
~r(a)
|
» |
p(a) | p(b)
|
|
|
+
|
~r(c)
|
» |
p(c) | p(b)
|
|
|
+
|
~p(S)
|
» |
r(Y) | p(b)
r(Y) | p(Y)
r(b)
|
| p(b) | r(Y) | p(b)
|
+
|
~p(S) | p(b)
|
» |
r(Y) | p(b) | p(b)
p(b) | r(Y) | p(b)
r(b) | p(b)
|
|
|
+
|
~p(b)
|
» |
r(Y) | p(b)
p(b) | r(Y)
r(Y)
|
|
|
+
|
~r(a)
|
» |
p(b) | p(b)
|
|
|
+
|
~r(c)
|
» |
p(b) | p(b)
|
|
|
+
|
~p(S)
|
» |
r(Y) | p(b)
p(b) | r(Y)
r(b)
|
| r(Y) | p(b)
|
+
|
~p(S) | p(b)
|
» |
r(Y) | p(b)
|
|
|
+
|
~p(b)
|
» |
r(Y)
|
|
|
+
|
~r(a)
|
» |
p(b)
|
|
|
+
|
~r(c)
|
» |
p(b)
|
|
|
+
|
~p(S)
|
» |
r(Y)
|
| r(Y) | p(Y)
|
+
|
~p(S) | p(b)
|
» |
r(Y) | p(b)
|
|
|
+
|
~p(b)
|
» |
r(b)
|
|
|
+
|
~r(a)
|
» |
p(a)
|
|
|
+
|
~r(c)
|
» |
p(c)
|
|
|
+
|
~p(S)
|
» |
r(Y)
|
| p(b) | r(b)
|
+
|
~p(S) | p(b)
|
» |
r(b) | p(b)
|
|
|
+
|
~p(b)
|
» |
r(b)
|
|
|
+
|
~p(S)
|
» |
r(b)
|
| p(b) | p(a)
|
+
|
~p(S) | p(b)
|
» |
p(a) | p(b)
p(b) | p(b)
|
|
|
+
|
~p(b)
|
» |
p(a)
|
|
|
+
|
~p(S)
|
» |
p(a)
p(b)
|
| p(b) | p(c)
|
+
|
~p(S) | p(b)
|
» |
p(c) | p(b)
p(b) | p(b)
|
|
|
+
|
~p(b)
|
» |
p(c)
|
|
|
+
|
~p(S)
|
» |
p(c)
p(b)
|
| 3rd ply
|
| Lots and lots
|
| p(b)
|
+
|
~p(b)
|
| |
» |
FALSE
|
|
Clearly things can get out-of-hand very quickly.
The total number of clauses typically grows exponentially with the number of
plys.
It is necessary to:
- Be selective about which resolvants are generated when.
- Use restriction strategies to prevent certain resolvants from
being generated.
A common effect of restrictions is to force a longer refutation while
restricting the choices.
- Use deletion strategies to delete unnecessary clauses.
The ANL Loop
The ANL loop is a flexible algorithm for controlling the generation
of inferred clauses.
Let CanBeUsed = {}
Let ToBeUsed = Input clauses
While Refutation not found && ToBeUsed not empty
Select the ChosenClause from ToBeUsed
Move the ChosenClause to CanBeUsed
Infer all possible clauses using the ChosenClause and other clauses from CanBeUsed.
Add the inferred clauses to ToBeUsed
Depending on how the ChosenClause is selected from the
ToBeUsed set, different search strategies can be implemented.
- Depth first search
- Select a most recently created resolvant as the
ChosenClause.
- Does not guarantee a complete search (could get into an infinite loop)
- Does not guarantee finding the shortest refutation.
- Breadth first search
- Select a least recently created resolvant as the
ChosenClause.
- Will find the shortest refutation.
- Implements a ply-by-ply search.
- Best first search
- Select the 'best' clause as the ChosenClause.
the best possible literals.
- The notion of "best" is determined by a heuristic function.
| Example to try with BFS and DFS
|
|---|
S1 = { p(f(X)) | q(Y),
p(X) | q(d),
p(f(d)) | ~q(X),
~p(f(X)) }
|
Exam Style Questions
- Write out the ANL loop algorithm.
- Show the execution of the ANL loop to derive the empty clause from:
S = { ~r(Y) | ~p(Y),
p(b),
r(a),
p(S) | ~p(b) | ~r(S),
r(c) }
Use any selection strategy you want, and number the chosen clause at
each iteration.