Interpretation
In the discussion above, the word "meaning" keeps coming up.
It is necessary to formalize what is meant by "meaning", as used in the above informal definition
of logical consequence.
An interpretation defines one meaning of symbols, functions, and statements.
An interpretation of a language takes the words used (the syntax) and associates them with the
objects that they represent.
(That such an association is necessary for intelligent action is motivated in Newell and Simon's
Turing Award paper [NS76], and that association motivates the use of semantics for search
guidance.)
Similarly, functions of the language are applied to objects in the world, and are evaluated to
objects in the world.
Finally, statements are evaluated as either true or false.
Interpretation of statements
The words of statements are given an interpretation by associating each different part with an
object in a set called the domain of the interpretation.
Functions are given an interpretation by applying them to elements of the domain and assigning
a result from the domain.
Statements and connected statements are then interpreted using the interpretations of the
component parts and the connectives.
| Example
|
|---|
man → 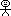 mortal →
mortal →  fly →
fly → 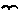 Socrates →
Socrates → 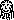 Xanthippe →
Xanthippe → 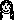 Spouse of
Spouse of 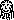 → → 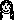 Spouse of
Spouse of 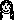 → → 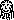 All
All 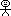 are are  → TRUE → TRUE
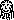 is a is a 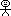 → TRUE → TRUE
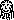 is is  → TRUE → TRUE
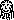 could could 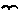 → FALSE → FALSE
|
Interpretation of connectives
Connectives are the words that join together nouns and verbs, e.g.,
and, or, all.
There are 16 binary and 4 unary connectives.
In English we have an intuition of their meaning (interpretation).
In logic their intepretation is formally defined.
Interpretation of statements
Statements are interpreted by first interpreting the words, then the
sentences without connectives, and then the full sentence.
For example,
All men are mortal or Socrates could fly
All 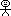 are
are  or
or 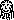 could
could 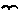
TRUE or FALSE
TRUE
Models, satisfiability, unsatisfiability
There are some definitions that make it easy to discuss the relationships
between formulae and interpretations.
Learn these words!
An interpretation is a model of a formula (set of formulae) iff the formula (the
conjunction of the formulas in the set) is TRUE in the interpretation.
For example, the interpretation above is a model of the formula All men are mortal, and
of the set of formulae {All men are mortal, Socrates is a man, Socrates is mortal}.
A formula (set of formulae) is satisfiable iff it has a model.
For example, the formula All men are mortal, and the set of formulae
{All men are mortal, Socrates is a man, Socrates has a beard}, are satisfiable.
A formula (set of formulae) is valid (also called a tautology) iff every
interpretation is a model.
For example, the formula Socrates is mortal or Socrates is not mortal is valid.
Valid formulae are also called tautologies, written |=.
The example is written |= Socrates is mortal or Socrates is not mortal.
A formula (set of formulae) is counter-satisfiable iff it's negation has a model.
For example, the formula All men are mortal, and the set of formulae
{All men are mortal, Socrates is a man, Socrates has a beard} are counter-satisfiable.
A formula (set of formulae) is unsatisfiable (also called a contradiction) iff
it has no models.
For example, the set of formulae {All men are mortal, Socrates is a man, Socrates is not
mortal} is unsatisfiable (if you think about it, but it will be proved formally later).
Logical Consequence
Now that the notion of "meaning" has been formalised as interpretation, it is possible to
formalize logical consequence - a conjecture that is TRUE independent of the meaning of the
statements used.
An alternative way of looking at logical consequence, as opposed to the conjecture being TRUE
independent of the meaning, is to think of logical consequence as a conjecture that is TRUE for
all possible meanings.
If it is TRUE for all possible meanings then you can ignore the meaning, because it doesn't matter
which one you choose.
This is the idea used here.
The formal definition of logical consequence is then:
A conjecture is a logical consequence (a theorem) of a set of axioms if (and only if)
every model of axioms is also a model of the conjecture.
Notice the use of the word "every".
That's what captures the ideas of "all possible meanings".
For all possible meanings of the symbols used, if the are TRUE then the conjecture is TRUE.
The form used for writing the axioms and logical consequence is Axioms |= Theorem.
The definition requires access to "every model of the axiom set".
Is this possible?
Consider again the very first example:
| Example
|
|---|
A = { All men are mortal,
Socrates is a man }
C = Socrates is mortal
|
The deduced formula is apparently a logical consequence of the axioms, i.e., the symbols
(man, mortal, Socrates) and the statements given can have any
interpretation, and the conjecture will still be TRUE in that context.
The intended interpretation (and model of the axiom set) is :
man → 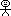 mortal →
mortal →  Socrates →
Socrates → 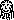 All
All 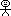 are
are  → TRUE
→ TRUE
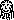 is a
is a 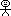 → TRUE
→ TRUE
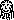 is
is  → TRUE
→ TRUE
and it is TRUE that Socrates is mortal.
That makes sense, and that's what is intended.
That "checks" one model of the axiom set.
Another model of the axiom set is:
man →  mortal → $$$
Socrates →
mortal → $$$
Socrates →  All
All  are $$$ → TRUE
are $$$ → TRUE
 is a
is a  → TRUE
→ TRUE
 is $$$ → TRUE
is $$$ → TRUE
Here the axiom All men are mortal means every motor car is expensive, and
Socrates is a man means a Corvette is a motor car.
The conjecture Socrates is mortal means that a Corvette is expensive.
Again the conjecture makes sense.
That's another model checked.
This process of checking models of the axiom set must continue for "every model of the axiom set".
In general, there can be an infinite number of models, and so there appears to be a problem here,
but this will be discussed and overcome in the context of propositional and 1st order logic, later.
However, it is the case that the conjecture Socrates is mortal is a logical consequence
of the axioms All men are mortal and Socrates is a man (unless you change what
is meant by the connective all).
In the argument form:
{All men are mortal, Socrates is a man} |= Socrates is mortal.
Checking for Logical Consequence
Generically, the process of checking for logical consequence can be thought of as checking rows
of a table.
There is one row of the table for each possible interpretation of the formulae, and a column for
each axiom and a column for the conjecture.
Then, for each row which is a model of all the axioms columns, it is necessary to check that the
row is a model of the conjecture column.
If this check always succeeds then the conjecture is a logical consequence of the axioms.
| Interpretation | Axiom 1 | Axiom 2 | ... | Conjecture
|
|---|
| 1 | Model | Model | all models | Model
|
| 2 | Model | Model | all models | Model
|
| 3 | Model | Not model | ... | Doesn't matter
|
| 4 | Model | Model | all models | Model
|
| 5 | Not model | ... | ... | Doesn't matter
|
| ... | ... | ... | ... | ...
|
| ? | Model | Model | all models | Model
|
Note that it is necessary to check the conjecture column only for those rows that are models of
all the axiom columns.
Other rows are not relevant to this process.
If the axiom set has no models (i.e., it is unsatisfiable) then vacuously every conjecture is a
logical consequence of the axiom set.
(Relevance logics are designed to avoid this paradox.)
In practical application of ATP it is sensible to check that axiom sets used are satisfiable,
e.g., by building a model of the axioms.
| Interpretation | Axiom 1 | Axiom 2 | ... | Conjecture
|
|---|
| 1 | Model | Not model | ... | Doesn't matter
|
| 2 | Not model | ... | ... | Doesn't matter
|
| 3 | Model | Not model | ... | Doesn't matter
|
| ... | ... | ... | ... | ...
|
| ? | Model | Not model | ... | Doesn't matter
|
Logical Consequence by Unsatisfiability
The method for checking for logical consequence given above requires checking that each model
of the axioms is a model of the conjecture.
If the conjecture is a logical consequence, then no interpretation will be a model of both the
axioms and the negated conjecture.
That is, the set consisting of the axioms and the negated conjecture has no models, i.e., is
unsatisfiable.
A conjecture is a logical consequence of a set of axioms iff every model of the axioms is not a
model of the negation of the conjecture, i.e., if Axioms ∪ {~Conjecture} has no
models, i.e., if Ax ∪ {~Conjecture} is unsatisfiable.
| Interpretation | Axiom 1 | Axiom 2 | ... | ~ Conjecture
|
|---|
| 1 | Model | Model | all models | Not model
|
| 2 | Model | Model | all models | Not model
|
| 3 | Model | Not model | ... | Doesn't matter
|
| 4 | Model | Model | all models | Not model
|
| 5 | Not model | ... | ... | Doesn't matter
|
| ... | ... | ... | ... | ...
|
| ? | Model | Model | all models | Not model
|
If any row is a model of the axioms and the negation of the conjecture, then
the conjecture is not a logical consequence of the axioms.
| Interpretation | Axiom 1 | Axiom 2 | ... | ~ Conjecture
|
|---|
| 1 | Model | Model | all models | Not model
|
| 2 | Model | Model | all models | Not model
|
| 3 | Model | Not model | ... | Doesn't matter
|
| 4 | Model | Model | all models | Model
|
| 5 | Doesn't matter
|
| ... | Doesn't matter
|
| ? | Doesn't matter
|
Logical Consequence by Inference
An inference rule infers formulae from parent formulae.
An inference rule is sound if it infers only logical consequences of its parents.
The basic procedure is:
Put the axioms in a set
While the conjecture has not been found
Copy some formulae from the set
Use sound inference rules to generate logical consequences of the formulae
Put the logical consequences into the set
Note the "Copy", indicating that a fresh copy of a formula may be used multiple times.
An inference system is complete if, by repetitive use, it can infer every logical
consequence of its input.
Non-logical Consequence
The formal definition of logical consequence can be transformed into one of non-logical
consequence:
A conjecture is not a logical consequence of a set of axioms if some model of the axioms is not a
model of the conjecture.
or equivalently
A conjecture is not a logical consequence of a set of axioms if some model of the axioms is a model
the negation of the conjecture.
Here's an example of non-logical consequence:
| Example (of non-logical consequence)
|
|---|
A = { All men are mortal,
Socrates is a man }
C = Socrates has a beard
|
Semantically, this conjecture is correct; Socrates did have a beard.
There is indeed an interpretation that is a model of the axioms that is
also a model of the conjecture.
man → 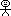 mortal →
mortal →  beard →
beard →  Socrates →
Socrates →  All
All  are
are  → TRUE
→ TRUE
 is a
is a  → TRUE
→ TRUE
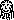 has a
has a  → TRUE
→ TRUE
However, there is another model of the axiom set that is not a model of the
conjecture:
man → 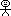 mortal →
mortal →  beard →
beard →  Socrates →
Socrates → 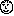 All
All 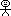 are
are  → TRUE
→ TRUE
 is a
is a  → TRUE
→ TRUE
 has a
has a  → FALSE
→ FALSE
The conjecture is not a logical consequence or the axioms because there is
a model of the axioms that is not a model of the conclcusion.
Equivalently, the conjecture is not a logical consequence or the axioms
because there is a model of the axioms and the negation of the conjecture:
man →  mortal →
mortal →  beard →
beard →  Socrates →
Socrates →  All
All  are
are  → TRUE
→ TRUE
 is a
is a  → TRUE
Not(
→ TRUE
Not( has a
has a  ) → TRUE
) → TRUE
Looking at a table of interpretations:
| Interpretation | Axiom 1 | Axiom 2 | ... | Conjecture
|
|---|
| 1 | Model | Model | all models | Model
|
| 2 | Model | Model | all models | Model
|
| 3 | Model | Not model | ... | Doesn't matter
|
| 4 | Model | Model | all models | Not model
|
| 5 | Doesn't matter
|
| ... | Doesn't matter
|
| ? | Doesn't matter
|
Decidability of Logical Consequence
A reasoning system for a given logic is decidable if it can determine whether or not a
conjecture is a logical consequence or is a non-logical consequence of a set of axioms.
Equivalently, a reasoning system for a given logic is decidable if it can determine whether a
set of formulae (e.g., the axioms and the negated conjecture) is satisfiable or unsatisfiable.
A reasoning system for a given logic is semi-decidable if it can determine that a
conjecture is a logical consequence of a set of axioms, but might not be able to determine that
a conjecture is a non-logical consequence of a set of axioms.
Equivalently, a reasoning system for a given logic is semi-decidable if it can determine that
a set of formulae is unsatisfiable, but might not be able to determine that a set of formulae is
satisfiable.
Exam Style Questions
- Define the following terms used in classical logic:
- Interpretation
- Model
- Satisfiable
- Unsatisfiable
- Logical consequence
- What does it mean for an inference system to be {sound, complete}?
- Explain how unsatisfiability can be used to establish logical consequence in classical logic.
mortal →
fly →
Socrates →
Xanthippe →
Spouse of
→
Spouse of
→
All
are
→ TRUE
is a
→ TRUE
is
→ TRUE
could
→ FALSE
are
or
could
mortal →
Socrates →
All
are
→ TRUE
is a
→ TRUE
is
→ TRUE
mortal → $$$ Socrates →
All
are $$$ → TRUE
is a
→ TRUE
is $$$ → TRUE
mortal →
beard →
Socrates →
All
are
→ TRUE
is a
→ TRUE
has a
→ TRUE
mortal →
beard →
Socrates →
All
are
→ TRUE
is a
→ TRUE
has a
→ FALSE
mortal →
beard →
Socrates →
All
are
→ TRUE
is a
→ TRUE Not(
has a
) → TRUE