Syntactic Refinements

Ordering

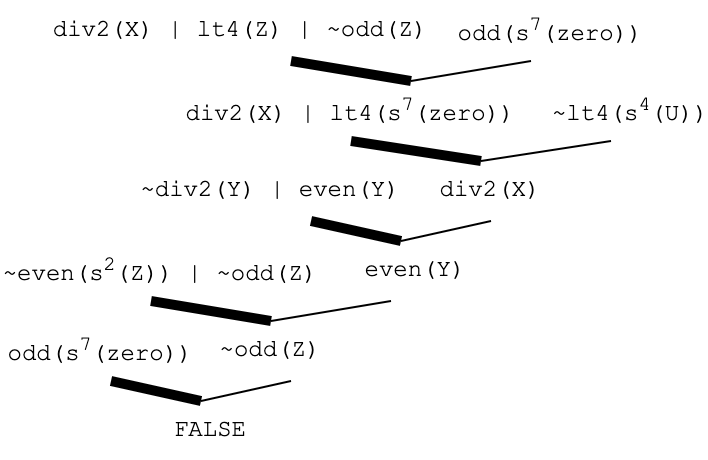
Example
S2 = { ~p(X) | q(X) | ~r(X), p(a) | p(b), ~q(Y), r(a), r(b) } HB = { p(a), p(b), q(a), q(b), r(a), r(b) } O = p(a) > p(b) > q(a) > q(b) > r(a) > r(b)

Notice all the possible resolutions that are prevented by the ordering strategy.

In the above example, the resolved upon literals all were or became ground in unification. Thus it was always possible to check that the largest Herbrand based literal was used in each clause. However, this is not always the case. If variables are unified then it is not necessarily known that the literal is the largest Herbrand based in the clause. An analogous problem arises if the ordering is not total, i.e., some pairs of terms or literals are not comparable.

Example
S1 = { p(b) | r(Y) | p(Y), ~p(S) | p(b), ~p(b), ~r(a), ~r(c) } HB = { p(a), p(b), p(c), r(a), r(b), r(c) } O = p(a) > p(b) > p(c) > r(a) > r(b) > r(c)

Here is the proof tree for the first part of a derivation.

If ~r(a) is used to complete the refutation, the proof does not conform to the ordering restriction at the first resolution. Here's the proof tree with variables instantiated up the tree. Note that p(a) is the largest atom in p(b) | r(a) | p(a)

However, until the time of that last inference, it is not known at the time what value the variable X will instantiated to. Similarly, if ~r(c) is used in the last step instead of ~r(a) then it will still not conform. A proof tree that conforms is:

The solution is to do restrospective checks (which is very expensive), or do ordering on only the predicate symbols (which is easy but less restrictive), or use a ground completable ordering (which is harder but more restrictive). Read on ...

Example
S2 = { ~p(X) | q(X) | r(X), p(a) | p(b), ~q(Y), ~r(a), ~r(b) } O = p/1 > q/1 > r/1

Ordering is a refutation complete strategy

Knuth-Bendix Ordering

A reduction ordering is ...

• Stable under substitution, i.e., if T1 > T2 then T1θ > T2θ
• Stable under context, i.e., if T1 > T2 and T3[P] then T3[T1] > T3[T2] for an arbitrary subterm P
• Terminating, i.e., there is no infinite sequence of terms T1 > T2 > T3 > ....  Note that it is possible to have a sequence T1 < T2 < T3 < ....

• For a term S[P], S > P, i.e., a term is larger than all of its subterms.

F = { joe/1, kevin/1, turkey/0, chicken/0 }

An ordering R is ground complete if for all pairs of ground terms or atoms (elements of the Herbrand Universe or Herbrand Base) HUT₁ and HUT₂, one of the following holds ...

• HUT₁ <_R HUT₂
• HUT₁ is HUT₂
• HUT₁ >_R HUT₂

An (simplification) ordering O is ground completable if there exists a ground complete reduction ordering R such that O is a subset of R, i.e., the pairs of terms ordered by O are ordered the same by R, and R may order some more pairs of terms that are not ordered by O.

Knuth-Bendix Ordering is an example of a simplification ordering. It is not ground complete, but is ground completable. KBO uses a precedence ordering ρ and a weighting function ω.

• ρ totally orders the predicate and function symbols, and does not order variables wrt anything.
• ω maps each predicate and function symbol to a non-zero positive integer, and maps all variables to the same positive number less than or equal to the mapping of any constant symbol. ω then maps a term T to the sum of the mappings of the symbols in T.

• Every variable in T2 occurs at least the same number of times in T1

  and

• ω(T1) > ω(T2)
  or
• ω(T1) = ω(T2) and ρ(symbol_of(T1)) > ρ(symbol_of(T2))
  or
• ω(T1) = ω(T2) and symbol_of(T1) ≡ symbol_of(T2) and args(1 .. i-1,T1) ≡ args(1 .. i-1,T2) and args(i,T1) > args(i,T2)

Example

S = { even(sum(two_squared,b)), two_squared = four, ~zero(X) | difference(four,X) = sum(four,X), zero(b), ~even(difference(two_squared,b)) } ρ : even > zero > = > sum > difference > four > two_squared > b ω(even) → 5 ω(zero) → 5 ω(=) → 3 ω(sum) → 4 ω(difference) → 3 ω(four) → 4 ω(two_squared) → 4 ω(b) → 3 ω(X) → 1 ω(even(X)) → 6 ω(zero(X)) → 6 ω(difference(four,X)) → 8 ω(sum(four,X)) → 9 ω(difference(four,difference(four,four))) → 18 ω(difference(four,X) = sum(four,X)) → 20 sum(four,X) > difference(four,X) sum(four,X) = difference(four,X) > zero(X) even(X) > zero(X) even(sum(X,four)) > even(sum(X,two_squared)) even(sum(X,four)) !> even(sum(four,two_squared)) even(sum(X,four)) !> even(sum(Y,two_squared)) difference(four,difference(four,four)) !> sum(four,X)

KBO can be used to identify literals in a clause that are known to be smaller than another, clause according to their atoms. An optional additional rule is that if a positive and negative literal are identical then the positive one is smaller. If there is equality in the problem and the system uses built-in equality reasoning (see later), then the comparison by arguments must not be used when comparing two equality literals (or must take into account the symmetry of the arguments). This is discussed in the section on equality. The KBO weighting function ω can also be used for clause selection in the ANL loop.

Example, using KBO for everything

ω maps all predicates and function symbols to 2, and all variables to 1. ρ is alphabetic S10 = { ~p(a) [4] ~q(W) | s(W) [6] ~s(X) | p(a) [7] (Subsumed by ~s(X)) ~r(Y) | s(Y) [6] p(Z) | q(Z) | r(Z) } [9] ~p(a) is the ChosenClause ~q(W) | s(W) is the ChosenClause ~r(Y) | s(Y) is the ChosenClause ~s(X) | p(a) is the ChosenClause (Subsumed by ~s(X)) + ~p(a) » ~s(X) [3] ~s(X) is the ChosenClause p(Z) | q(Z) | r(Z) is the ChosenClause + ~p(a) » q(a) | r(a) [8] q(a) | r(a) is the ChosenClause + ~q(W) | s(W) » r(a) | s(a) [8] r(a) | s(a) is the ChosenClause (Subsumed by s(a) | s(a)) + ~r(Y) | s(Y) » s(a) | s(a) [8] s(a) | s(a) is the ChosenClause + ~s(X) » FALSE

Other Orderings

Lock Resolution

Example
S1 = { p(b)1 | r(Y)2 | p(Y)3, ~p(S)4 | p(b)5, ~p(b)6, ~r(a)7, ~r(c)8 }

Notice the marked reduction of the search space.

Example
S2 = { ~p(X)1 | q(X)2 | r(X)3, p(a)4 | p(b)5, ~q(Y)6, ~r(a)7, ~r(b)8 }

Example
S = { bf(a), ~bg(a), ~bf(X) | bh(X), ~bj(X) | ~bi(X) | bf(X), ~bh(X) | bg(X) | ~bi(Y) | ~bh(Y), bj(b), bi(b) }

Lock resolution is a refutation complete strategy

Proof
To be filled in.

Exam Style Questions

1. Show the execution of the ANL loop implementing unit resolution, and then unit resulting (UR) resolution, to derive the empty clause from the following. Use subsumption, writing the subsuming clause next to the crossed out subsumed clause.

   S2 = { ~p(X) | q(X) | r(X),
          p(a) | p(b),
          ~q(Y),
          ~r(a),
          ~r(b) } 

   S11 = { p(X) | ~p(f(X))
           ~p(a)
           p(S) | q(S) | r(S)
           ~q(T) | p(a)
           ~r(T) | p(a) } 

2. Neither of the clause sets in the previous question are Horn. How can you be assured that unit and UR resolution will work for them?

3. What is the relationship between unit resulting and UR resolution?

4. Explain the constaint imposed by ordered resolution.

5. Show the execution of the ANL loop implementing ordered resolution, using least symbol count as the selection strategy. Use reverse dictionary order for the ordering on the Herbrand Base. Use pure literal deletion, tautology deletion, and subsumption. Write the subsuming clause next to the crossed out subsumed clause.

   S2 = { ~p(X) | q(X) | r(X),
          p(a) | p(b),
          ~q(Y),
          ~r(a),
          ~r(b) } 

   S11 = { p(X) | ~p(f(X))
           ~p(a)
           p(S) | q(S) | r(S)
           ~q(T) | p(a)
           ~r(T) | p(a) } 

6. The ordered resolution restriction is on the completed refutation. What difficulty does that cause? What are two possible solutions?

7. Explain the four properties of a simplification ordering.

8. Given an ordering ρ or the predicate and function symbols, and a weighting function ω mapping each predicate and function symbol to a non-zero positive integer, mapping all variables to the same positive number less than the mapping of any function or predicate symbol, describe how two terms are ordered by Knuth-Bendix Ordering (KBO).

9. For reverse alphbetic ρ and ω mapping all predicates to 3, all functions to 2, and all variables to 1, determine the order between all pairs of the following atoms:

   p(f(X),X)        p(f(X),Y)      p(a,X)        q(f(X),X)     q(f(a),X)
   p(f(a),a)        p(X,Y)         q(X,Y)        q(X,X)        p(a,a) 

10. Show the execution of the ANL loop implementing ordered resolution, using KBO weight as the selection strategy. Use KBO order for the ordering on the Herbrand Base, with ω mapping all predicates to 3, all functions 2, and all variables to 1. ρ is reverse alphabetic. Use pure literal deletion, tautology deletion, and subsumption. Write the subsuming clause next to the crossed out subsumed clause.

    S = { t(a)
          ~t(Z) | q(Z) | r(Z)
          ~q(W) | ~p(W)
          p(X) | ~t(a)
          ~r(Y) | ~p(Y) } 

    (Disclaimer - I have not worked out the answer to this exercise, so it may go weird on you. Bug reports are welcome :-)