On Enigma and a Method for its Decryption

Author: Harald Schmidl



Abstract:

The present paper investigates and describes the German mechanical cipher machine called Enigma, and presents a possible way to its decryption. During World War II, the Germans used a typewriter-like machine named Enigma to encrypt military messages. We make an attempt at a historical introduction, and non-technical background information is provided. This paper includes a C program that simulates Enigma, and a method to break its code. The latter is achieved by a simulation of a simplified Bombe, a mechanical device that was actually used during WWII at Bletcheley Park, a site in England where a major deal of the work on breaking Enigma's code was done. Much of the credit for breaking the code must be given to a group of accomplished Polish mathematicians, and the famous, and in the computer community well known mathematician Alan Turing.

Keywords: Enigma, Bombe, Cryptography

Some History:

The principle behind Enigma is rather old. Mechanical ciphering devices based on rings and cylinders have been described as early as in the 4th century B.C. The Roman Aeneas Tacitus talked about a cipher disk and its usage [6]. Enigma was patented by Arthur Scherbius in 1918, an inventor who thought of it as a ciphering device for businesses that needed to communicate confidential documents. The German military caught interest, and commercial production was stopped in 1923 [6]. The initial idea was pretty much based on the well known Caesar cipher [7], a mono-alphabetic substitution. Each letter is substituted for example by its n-th neighbor in the alphabet.

ABCDEF...
CDEFGH...

DEAF becomes FGCH in this example where each letter is replaced by its n+2 neighbor (wrap around after Z!). The code however is easy to break. Scherbius came up with a better idea, which led to the use of a poly-alphabetic scheme. Each time a letter is encoded, also the number n changes. For example,

ABCDEF... first letter to encode
CDEFGH...

ABCDEF... second letter to encode
DEFGH I...

ABCDEF... third letter to encode
EFGH I J...

ABCDEF... fourth letter to encode
FGH I J K...

Thus, DEAF becomes FHEK. Although both encodings are similarly far from the original, the latter technique enhances the security of the code since it does alter the encoding scheme.

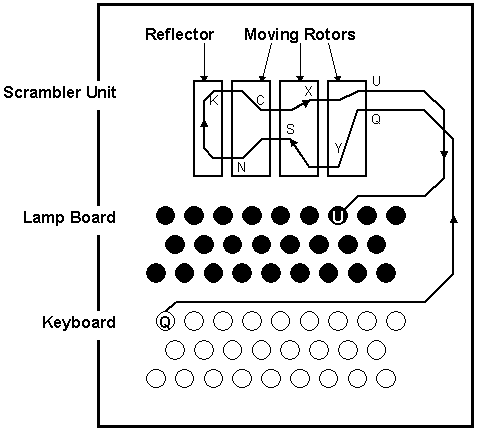
The following image shows a sketch of the interior design of Enigma [1].

The main units consist of a keyboard, the scrambler unit and the lamp board. The encoding is done in the scrambler unit. It holds a number of rotors with 26 contacts (A-Z) left and right of the rotor. Each left contact is connected to a contact on the right by an internal wiring scheme. Rotors are connected with each other by sliding contacts. A reflecting rotor mirrors the connection backwards. Depending on the relative position of the rotors, a current flows on a certain path from right to left through all the rotors, is reflected and passed back to the right side. The entry point corresponds to a letter in plain text, the exit point accordingly to a letter in cipher text. By using the reflecting rotor, the handling of the machine is simplified. If A is encoded to say E, then the reverse is also true. Therefore the same machine can be used for encoding and decoding without any rewiring necessary [1].
The message is typed in like on a typewriter. Each time a key is hit, current flows through the contacts in the scrambler unit and illuminates a lamp with the enciphered letter showing. After a key was pressed, the rightmost rotor changes its position by a 1/26 rotation. Like in an automobile's odometer, after a full rotation of the rightmost wheel, also the middle wheel changes by a 1/26 rotation, and accordingly the leftmost after the middle wheel has made one full rotation. Little notches on the rotor's sides take care of that. To decrypt a message, one needs not only an Enigma machine, but also the knowledge of the starting state, i.e. at which positions the wheels were when the text was typed in. To decrypt the message, the machine must be set to the same starting state, and the cipher text is entered. Output is the plain text.
Given the current and original Enigma setup, we yield 26x26x26 = 17,576 possible starting states. To enhance the security of Enigma, five rotors with different internal wirings were in use. Any three of these could be used in the machine in any order. We arrive at 17,576x60 = 1,054,560 possibilities. The rotors had letters on their outer rim. This rim was moveable, giving the ring positions. Basically, the rings allow shifting the relative position of letters shown to internal core wiring of the rotor. Exactly the same position of the wheel can now show a different letter. A further gain of security is added by implementing the so called Steckerboard. Before the letters get to the scrambler unit, they may be swapped by cross-connecting them. Connecting A with say E by a plug swaps A with E and vice versa. Using a number of plugs around 5 or 6 (maximun 13) raises the possible states by a factor of 2-3 billion. With the methods given at these days, i.e. trying keys manually, Scherbius calculated that 1000 operators would have to sit several million years to try all starting states. This led the German officials to the claim that their codes were unbreakable and safe [6].
To summarize, Enigma's security relies on the rotor settings, the ring settings, and the Steckerboard connections. For completeness, the following image shows a real Enigma.

Usage:

Slightly different Enigmas were in use. The German Navy used a somewhat more sophisticated model then the Army. A model with four rotors was developed, features to enhance security were added during the life of Enigma, and the way how to use it was altered frequently [1]. Some basic guidlines and features stayed mostly the same though.
The basic settings were written down in a code book, and changed daily. Basic settings are the rotors in use and their arrangement, the ring settings, and the Stecker connections. The user picked a random starting position for the wheels. It was transmitted as part of the message. Messages had a header consisting of sender, time, date and a code for recipient. Possible recipients were Army, Navy etc. Using codes made clear if a message needed to be decoded by the interceptor at all, i.e. if it was of any concern to him. The header was transmitted en clair. The sender then picked another random starting position for the wheels, encoded it, and included it twice after the message header. Therefore the two triples of letters after the header gave the recipient, when decoded according to the code book, the actual position of the wheels to which Enigma needed to be set for decoding the text. After that, the message body was appended. Messages were supposed to be shorter than 200 characters. The longer a message, the more likely it was for it to be broken. If needed, messages were split into pieces. Each piece was then encoded with a different key. There were certain conventions how to separate parts, words, make paragraphs and so on. The letter combination CH is very frequent in German, similar to TH in English, so it was abbreviated as Q. Words were separated with X. Numbers had to be spelled out and so forth [6].
Decoding of a message made necessary the possession of an Enigma machine, the starting state, and the knowledge of how to use the machine.

Breaking the Code:

With all its perfection, especially for the time, there were also flaws in Enigma. The human factor, and not to underestimate the belief in its being unbreakable eventually led to the code being cracked. Untrained and lazy radio staff used bad keys like keyboard diagonals and abbreviated swear words [6]. The whole concept of transmission with the doubly encoded starting position of the rotors had weak points. Knowing this gave the code breakers an entry point into Enigma's big secret. Many messages started in a similar way, say 'ANXGENERAL...'. 'AN' is German for 'TO', and 'X' is a word separator. Knowing parts of a message in plain text and cipher text was called a crib. Cribs are starting points for the attack on breaking the codes.
First and successful attempts at Enigma were being done by the Poles. After WWI, Poland kept an eye and ear on Germany by intercepting radio messages from the German Navy which was active around Polish shores. In 1926, when suddenly those messages became no longer understandable, it was clear that Germany had started to employ some ciphering scheme [6]. There is some myth aroud how Poland found out about what was behind these codes. It was likely a combination of espionage and simply luck how they found out about the electro-mechanical ciphering machine Enigma. It is said that some factory workers and even money needing German officials sold their knowledge. Another incident might be when Germany sent an Enigma accidentally by regular mail, and the Polish secret service had time over a weekend to inspect the machine. It is however without a doubt majorly the achievement of a number of talented young Polish mathematicians to aquire the deeper knowledge on how to use Enigma [5]. The commercial Enigma was not of too much help, but gave some clues on how the machine supposedly worked.
Poland may have bought some messages in plain text and cipher text, but they knew little about the rotor wiring at first, and without starting keys, no message could be deciphered. The mathematician Rejevski came up with a method to find the rotor wiring using linear algebra. All these little clues together gave them enough knowledge to build models of Enigma, and finally a replica. Furthermore, knowing that the first six letters were two equal triples of letters when decrypted helped him develop a scheme, that when analyzing many messages of the same day allowed coming up with the initial settings. It involved the usage of socalled Zygalski sheets. Perforated paper sheets were arranged on an illuminated table and revealed possible starting states. These starting states had then to be tried on an Enigma replica [1][6].
Over the years, the rotor wiring and the usage of Enigma was altered. This made some of the Polish developments obsolete, and they basically had to start all over again. The dual encoded message key at the beginning of a message was changed to singly transmitted key at some point shortly before the war.
A more sophisticated technique for code breaking was given by an electro-mechanical device named Bomby. Having a crib, i.e. a part of a message in plain text an code as given by the frequently similar message starts we can make certain deductions. There will only be a limited number of starting states that allows a crib. Too many for a human to try manually, but feasible for a machine. The machine steps through all possible starting states and stops when a match for the given crib is found. For three rotors, six Bombys were needed, corresponding to the six permutations [6].
In 1938, two more rotors were added. Three of which were in use at a time. The resulting 60 permutations would have required 60 Bombys. Poland didn't have the monetary ressources at that time to produce that many of their machines. When Poland was attacked by Germany, the heads of the code cracker team fled the country, and all their knowledge went to France and England. Some of the Polish mathematicians cooperated with especially the English in refining the strategies that finally led to cracking the code of Enigma.

Bletchley Park and the Bombe:

After the Polish had done that much quality work, England could take a head start on solving the riddle. The Government Communication Headquarters were located in Bletchley Park about 40 miles north of London, and employed about 10,000 people at the end of the war. The most famous among them were Alan Turing and Gordon Welchman, two mathematicians.
Benefiting from the knowledge aquired by the Polish, England's work concentrated on refining the Bomby into the Bombe. It is said that the name stems from the clicking sound that the Bombe made when working on a crib, much like a timer bomb fuse. The Bombe in principle also iterates through the possible starting states, giving possible solutions for a crib. They achieved however a more efficient solution that allowed leaving out some states, thus speeding up the process.
The Bombe is described in some detail in [3]. The first Bombes relied on circular loops in the cribs, as in the following example where in position 1, E is encoded to X, then in position 4 X to W, in position 8 W to V, and in position 10 V back to E.
E..X...W.V...
X..W...V. E...
A collection of scrambler units worked in parallel on the parts of the crib. We would have four units for our particular crib. The scrambler units are set to appropriate starting states. Say the first to AAA, the second to AAD, the third to AAH, and the fourth to AAJ, corresponding to the position of the letter pairs in the crib (1, 4, 8, 10). The scramblers work on the crib in parallel, and move to the next starting states (AAB, AAE, AAI, AAK) if the present state is not good, i.e. does not allow the crib. Cascading the units speeds up the decoding process. A test register is responsible for revealing possible Stecker settings. We might set the reference wire on the test register to X. If we get an output X for a valid setup, then there was no Stecker substitution for X. If the output however was another letter Y, then there was a possible substitution X with Y and vice versa. Detecting a valid setup was known as a drop. The bombe stopped, an operator noted the possible setup, and moved the machine on. Not every drop however revealed a valid setup. Some drops were always false solutions.
The problem here is to find cribs of sufficient length that included loops. By adding a feature called diagonal board, this problem could be solved by creating artificial loops by an additional scrambler unit. Also some of the false drops could be removed by the diagonal board. This feature was introduced by Gordon Welchman.

Do it yourself:

The earlier described Bomby is basically implemented here. Code for an Enigma simulation is incorporated into a program of two parts. The first part is simply an Enigma that allows the encryption of a text. Starting states may be chosen freely. Five wheels are available, and a Steckerboard may be used. The second part needs as input an encoded text and a number of characters known to be the plain text, i.e. a crib. The program then iterates through all possible starting states, and announces possible setups. Stecker substitutions up to two letter pairs are also detected by forming all possible strings of length four consisting of nonredundant pairs. However, the program runs a long time when this feature is used. It finds the starting state reliably and in an acceptable amount of time when no Steckerboard is used, or the alphabet for Steckering is limited to say only six characters, A-F. Depending on the length of the crib, between one exact and many possible solutions are found. It is therefore vital to know that the encoded message actually makes some sense to some kind of humans. Knowing that the first two letters of e.g. FWXTU decode to HE, and finding the possible solutions HEMTP, HEXMA and HELLO gives us three starting states. Either we can assume the third with HELLO is the right one, or we have many messages encoded in the same key available on which we can test the three possible starting states, thus finding the right one.
It became clear during the tests, that the ring position is not cruxial when trying to find the starting state. Moving the rings relative to the core wiring of the rotors gives actually 26x26x26 equivalent states, and therefore 26x26x26 equivalent solutions. Inserting a rotor with Z up is the same as calling Z an A and inserting it with A up. It ends up in the same position! To decrypt a message we only need to know the relative positions. The objective is to find a solution which we can use for the decryption of a message, i.e. given an Enigma knowing how to set it up correctly. It is therefore sufficient to find the relative position of the rotors, no matter how these are called by changing the rings. We set the rings to AAA by default in the program therefore.

Click here for the complete code for the Enigma simulation and the simple Bomby (enigma.c). Compile this program with a suitable C-compiler. At the head of the file you find two #define statements. One defines MSGLEN, currently set to 80 for the maximum length of a message to encode. The other one is called TO, and is currently set to 'E'. This means Stecker substitutions are checked only within an alphabet consisting of 'A'..'E'. The purpose of this is to save running time ('A'..'Z' runs days!!), and serves demo purposes of the program. Change both values freely as desired.
Run the program by typing the file name of the executable. Without parameters, you will be prompted to enter the starting values. You may then encode a message. E.g. type HELLO, and yield FWXTU. To decode this , type the program name followed by the cipher code and a number of known characters in plain text. E.g. 'enigma FWXTU HE'. The program iterates through all possible starting states and outputs possible solutions as appropriate, i.e. the machine settings and what the decoded message would be for these settings.
IMPORTANT ADDITION: It has been noted that the decoding part of "enigma.c" works not with all Enigma simulators. You should not attempt to decode messages from arbitrary simulators. This is likely due to different rotor wiring as used in different simulators. My Enigma (first part of the program) was taken from the web, and used to write the Bombe. Encode a message with the first part, decode it with the second. Attempting to decode messages from different simulators is likely to fail!

Discussion:

As stated earlier, Enigma had its flaws. Yet it was a complex machine, and its intrinsics were broken starting with only very little knowledge. It is especially for the time and the possibilities given an accomplishment to come up with a mechanical machine that is fast enough to compute possible codes. The Bombe reminds in many ways of an early parallel processor. Limited in its capabilities, and with a hardwired program, but efficient and doing what it was supposed to do by only using wheels and some wires.
The present program tries to implement some of the Bombe's features in a more modern software solution. Codes are broken in acceptable time. To further refine the program, an efficient implementation of how to cope with the Steckerboard substitutions would be necessary.

Acknowledgments:

Credit must be given to the people who have websites about Enigma and its decryption. See references for detail. The images in this text were taken from some of them. Fauzan Mirza wrote a program to simulate Enigma, and a part of the code is used here.

References:

NOTE: These references worked at the time of writing this document (1998). Some of these links are possibly broken now.

[1] http://www.attlabs.att.co.uk/andyc/enigma/about_enigma.html, Andy Carlson's home page about general Enigma features

[2] http://www.cranfield.ac.uk/ccc/bpark/morebpark.htm, Computer Centre at the Cranfield University home page about Bletchley Park,

[3] http://www.geocities.com/CapeCanaveral/Hangar/4040/bombe.html, Nik Shaylor's home page about general Enigma features and the bombe

[4] http://www.turing.org.uk/turing/index.html, The Alan Turing Home Page

[5] http://www.gl.umbc.edu/~lmazia1/Enigma/enigma.html, Dr. Wladyslaw Kozaczuk writes about the Polish work on deciphering Enigma codes

[6] http://home.earthlink.net/~nbrass1/enigma.htm, Nautical Brass home page on history and usage of Enigma

[7] Network Security, Textbook for class